Summary

I've been thinking about Private Keys and what makes a private key, what do they look like, how big are they, how big are the numbers that make them up, why prime numbers, prime number predictability and things of this sort. In this post I'm going to talk a bit about this subject in the hopes that it will spur some deeper conversations and questions. Thanks for joining me!

For purposes of this document we will work with a 4096-bit RSA Private key.

Private Keys

Private Keys are critical components in multiple facets of cryptography. They are required for certificates and they are required for encryption. Keys are analogous to the combination of a safe, and if an attacker knows the combination to your safe, game over.

Private Keys are used to decrypt data.

Public Keys are used to encrypt data that only a private key can decrypt.

Public Keys are derived from the Private Key. There is a mathematical relationship between the Private and the Public Key that allows data to be encrypted by the Public and decrypted by the Private.

Generate a Private Key

Lets generate an RSA Private Key and then dig into it! We will use the cryptographers Swiss army knife, OpenSSL.

openssl genrsa -out rsa-private.key 4096

What does this private key file look like. It's quite simple, it is a text file that contains a header, footer and some Base64 text. There is a lot of text here and its nonsensical so I'm only going to show the first and last 5 lines.

cat rsa-private.key | head -n 5 && cat rsa-private.key | tail -n 5

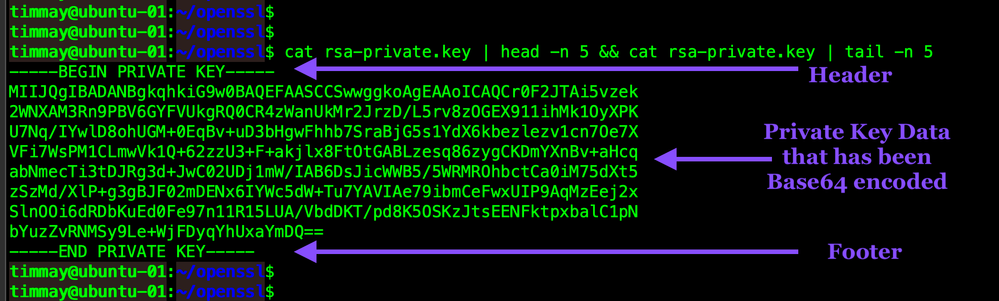
Decipher the Private Key

We can use OpenSSL to decipher this Base64 and see some useful things. The output here is a few pages long so I will paste a few snippets and explain each.

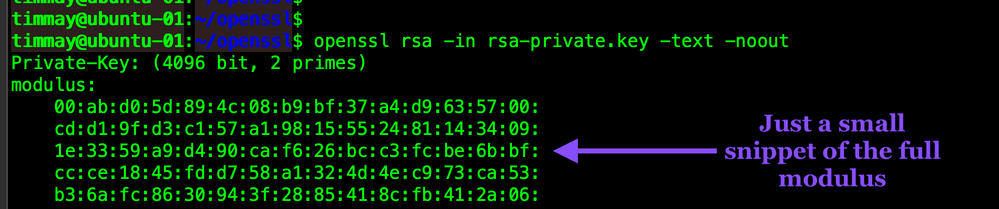
openssl rsa -in rsa-private.key -text -noout

There are a number of items in this file. We will see a modulus, a public and a private exponent, two primes, two exponents and a coefficient. Everything in this file is displayed as hex digits. Lets take a look at each item.

The Modulus

There is a modulus (n). The modulus is the product (multiplication) of both the primes and is an extremely large number, and because it is such a large number, it is extremely difficult to factor, which makes it extremely difficult to factor or crack. The same exact modulus is present in both the Private Key and in the Public Key.

The Public and Private Exponent

There is a public (e) and private exponent (d).

The public exponent (e) is part of the public key and is typically a small, fixed value, in my testing its always been 65,537. This integer is also the fourth Fermat prime aka F4.

The private exponent (d) is part of the private key and is used in conjunction with the private key for decryption operations. The private exponent is an extremely large number, typically the same size as the modulus.

The Primes

There are two prime numbers (p) and (q). These are very large numbers. They are represented as hex digits. We will display them in decimal format later. These are likely not normal prime numbers either, only specific types of prime numbers are good candidates for cryptography. Prime numbers that are good for cryptographic purposes include Sophie Germain and Safe Primes and Strong Primes.

Prime #1 (p)

Prime #2 (q)

The Exponents

There are two exponents. While these are labeled exponents these are really just the the prime minus 1. These exponents are used in Chinese Remainder Theorem (CRT). CRT is a math trick that helps when working with very large numbers, it basically takes one large math problem and breaks it down into several smaller problems with smaller numbers (I think).

Exponent#1 (dp) is equal to Prime #1 minus one. (dp) = (p) -1

Exponent#2 (dq) is equal to Prime #2 minus one. (dq) = (q) -1

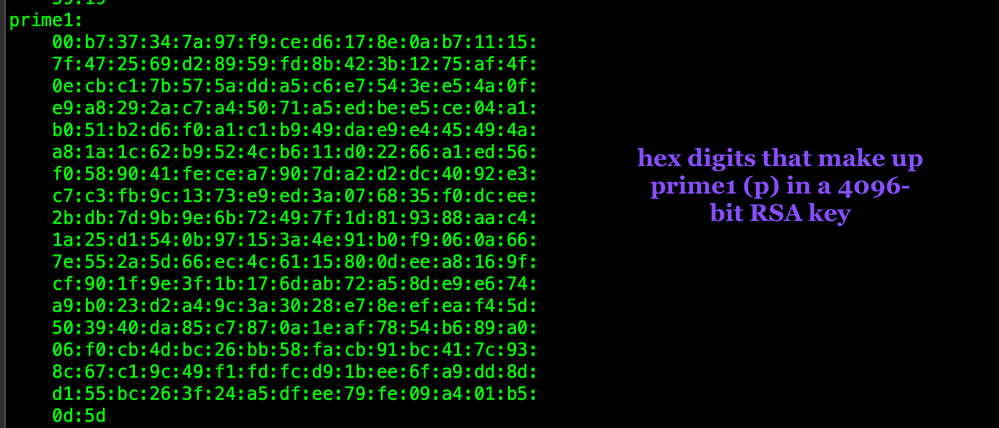
See here for Prime #1 and Exponent #1, they are just about the same size.

prime1:
00:b7:37:34:7a:97:f9:ce:d6:17:8e:0a:b7:11:15:7f:47:25:69:d2:89:59:fd:8b:42:3b:12:75:af:4f:0e:cb:c1:7b:57:5a:dd:a5:c6:e7:54:3e:e5:4a:0f:e9:a8:29:2a:c7:a4:50:71:a5:ed:be:e5:ce:04:a1:b0:51:b2:d6:f0:a1:c1:b9:49:da:e9:e4:45:49:4a:a8:1a:1c:62:b9:52:4c:b6:11:d0:22:66:a1:ed:56:f0:58:90:41:fe:ce:a7:90:7d:a2:d2:dc:40:92:e3:c7:c3:fb:9c:13:73:e9:ed:3a:07:68:35:f0:dc:ee:2b:db:7d:9b:9e:6b:72:49:7f:1d:81:93:88:aa:c4:1a:25:d1:54:0b:97:15:3a:4e:91:b0:f9:06:0a:66:7e:55:2a:5d:66:ec:4c:61:15:80:0d:ee:a8:16:9f:cf:90:1f:9e:3f:1b:17:6d:ab:72:a5:8d:e9:e6:74:a9:b0:23:d2:a4:9c:3a:30:28:e7:8e:ef:ea:f4:5d:50:39:40:da:85:c7:87:0a:1e:af:78:54:b6:89:a0:06:f0:cb:4d:bc:26:bb:58:fa:cb:91:bc:41:7c:93:8c:67:c1:9c:49:f1:fd:fc:d9:1b:ee:6f:a9:dd:8d:d1:55:bc:26:3f:24:a5:df:ee:79:fe:09:a4:01:b5:0d:5d

exponent1:
55:2b:0b:71:25:ae:91:70:c2:58:5c:30:c7:77:47:c8:49:e3:0c:64:9e:f9:96:bf:bd:f8:11:ce:e1:a0:4e:25:6d:f1:a8:a2:ba:4a:61:04:af:8c:24:c6:8a:e6:89:e4:82:13:a6:f5:7d:9d:ac:0c:e5:9d:0f:90:88:19:eb:82:c6:9e:e8:44:25:c8:6e:3d:ab:19:52:55:78:f6:87:91:73:69:7b:94:56:39:81:72:73:e4:9c:36:cb:06:e9:07:c9:ca:2d:63:79:d1:66:b7:0e:08:d3:b0:b4:f6:40:3a:ef:ab:bb:cc:bf:5f:e4:33:6c:ff:d1:d4:6d:bc:1d:e0:42:56:16:c0:04:29:ce:c1:df:b2:03:05:43:6f:ec:50:1b:85:57:42:84:6c:9b:a8:6a:ec:ca:51:a3:1b:bc:80:3d:7d:d3:ae:8c:6d:41:d5:6d:1e:69:e0:a8:3f:4e:28:4f:1f:bb:01:9a:88:bc:85:9a:be:0d:df:25:ed:33:27:f4:5a:60:4d:8d:11:47:f8:fd:94:3d:b9:71:e5:67:49:48:a3:91:51:e0:9b:e3:21:59:f6:93:a4:f6:6f:36:ba:dc:1c:eb:4a:7c:b1:4a:51:3c:97:98:5a:3e:0b:68:be:73:ed:57:96:28:b2:17:0b:a3:97:ec:e1:59:8d:d1:5d

The Coefficient

The coefficient is another very large number that is used during Chinese Remainder Theorem optimization processes and helps with the decryption process.

Supporting RFC

RFC3447 says the format of a private key is as follows.

RSAPrivateKey ::= SEQUENCE {
   version Version,
   modulus INTEGER, -- n
   publicExponent INTEGER, -- e
   privateExponent INTEGER, -- d
   prime1 INTEGER, -- p
   prime2 INTEGER, -- q
   exponent1 INTEGER, -- d mod (p-1)
   exponent2 INTEGER, -- d mod (q-1)
   coefficient INTEGER, -- (inverse of q) mod p
   otherPrimeInfos OtherPrimeInfos OPTIONAL

Large Numbers

In this document I've talked about extremely large numbers and very large numbers. Here I'd like to show how large some of these numbers actually are. Please remember we started this process with a 4096 bit RSA key which in 2023 is a pretty standard size.

Prime #1

Let's look at Prime #1 (p).

So how big is this number really?

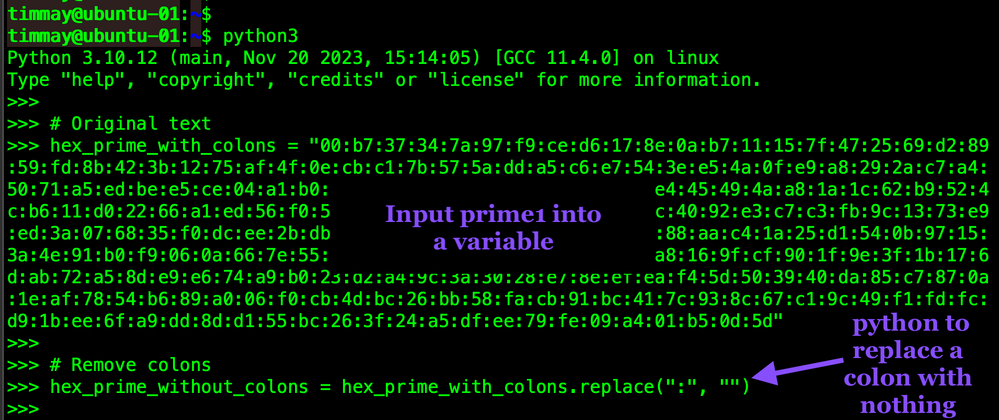
Lets take a look using some simple python code. First we will remove all the colons.

# prime1
hex_prime_with_colons = "00:b7:37:34:7a:97:f9:ce:d6:17:8e:0a:b7:11:15:7f:47:25:69:d2:89:59:fd:8b:42:3b:12:75:af:4f:0e:cb:c1:7b:57:5a:dd:a5:c6:e7:54:3e:e5:4a:0f:e9:a8:29:2a:c7:a4:50:71:a5:ed:be:e5:ce:04:a1:b0:51:b2:d6:f0:a1:c1:b9:49:da:e9:e4:45:49:4a:a8:1a:1c:62:b9:52:4c:b6:11:d0:22:66:a1:ed:56:f0:58:90:41:fe:ce:a7:90:7d:a2:d2:dc:40:92:e3:c7:c3:fb:9c:13:73:e9:ed:3a:07:68:35:f0:dc:ee:2b:db:7d:9b:9e:6b:72:49:7f:1d:81:93:88:aa:c4:1a:25:d1:54:0b:97:15:3a:4e:91:b0:f9:06:0a:66:7e:55:2a:5d:66:ec:4c:61:15:80:0d:ee:a8:16:9f:cf:90:1f:9e:3f:1b:17:6d:ab:72:a5:8d:e9:e6:74:a9:b0:23:d2:a4:9c:3a:30:28:e7:8e:ef:ea:f4:5d:50:39:40:da:85:c7:87:0a:1e:af:78:54:b6:89:a0:06:f0:cb:4d:bc:26:bb:58:fa:cb:91:bc:41:7c:93:8c:67:c1:9c:49:f1:fd:fc:d9:1b:ee:6f:a9:dd:8d:d1:55:bc:26:3f:24:a5:df:ee:79:fe:09:a4:01:b5:0d:5d"

# Remove colons
hex_prime_without_colons = hex_prime_with_colons.replace(":", "")

# Display the hex without colons
print(hex_prime_without_colons)

Now lets use some simple python code to convert this hex to a decimal number. Then print the decimal number in purple so it's easy to read.

# Convert hex prime to decimal format
decimal_prime = int(hex_prime_without_colons, 16)

#Add Purple Color Code
purple_color_code = '\033[95m'
reset_color_code = '\033[0m'

#Count the number of digits
number = len(str(decimal_prime))
print("Num of chars:", number)

print(f"Decimal Number: {purple_color_code}{decimal_prime}{reset_color_code}")

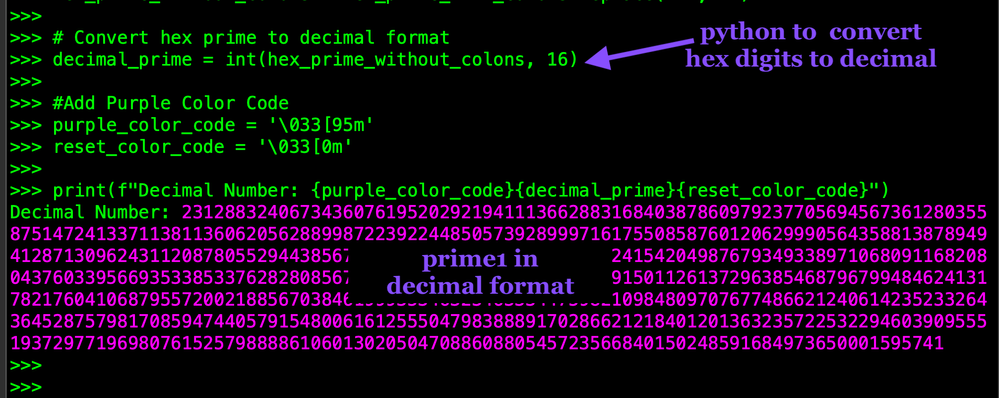
So that is prime1, it is 617 digits long. That is very large number.

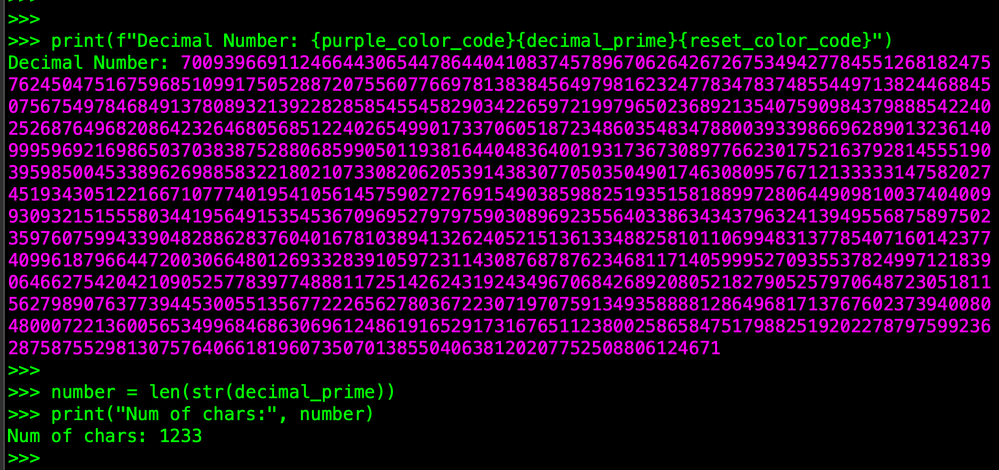
Modulus

If the primes are both about 617 digits long, well how long could the modulus be. I ran the same code above on the modulus and the modulus in my private key is 1233 digits long! That is an extremely large number.

Finally

Think about the largest number you can rationally fathom. Is it in the millions, billions, trillions, bazillions (I know that's not a thing). This is one quadrillion written out, 1,000,000,000,000,000. One quadrillion is a relatively small number when compared against the primes or the modulus in our private key.

Our modulus is a big number, it is much larger than a quadrillion, it's even larger than a googol, however its nowhere near as large as a googolplex. Even a googolplex is small when compared to Moser's Number, or Skewes's Number, or Graham's Number!!!

Googology is the study of nomenclature and properties of large numbers and I'm becoming fascinated by it.

In the PBS science program Cosmos: A Personal Voyage, Episode 9: "The Lives of the Stars", my favorite astronomer, Carl Sagan, estimated that writing a googolplex in full decimal form (i.e., "10,000,000,000...") would be physically impossible, since doing so would require more space than is available in the known universe.

If you are fascinated by key's and \ or large numbers write some comments below.

References

RFC 3447 - Public-Key Cryptography Standards (PKCS) #1: RSA Cryptography Specifications Version 2.1

Working with RSA Key Pairs

other ref's are linked inline.

Keys and Primes - A shallow dive into keys and very large primes

Table of Contents